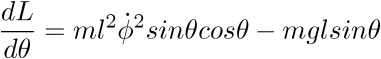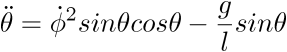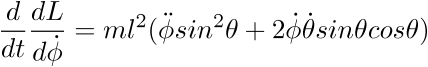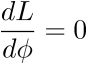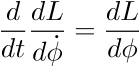Après avoir
déterminé les formes analytiques de l'énergie
potentielle Ep et l'énergie cinétique Ec nous calculerons le Lagrangien de
notre système grâce à la formule L=Ec-Ep
puis déterminerons les équations du mouvement des différents, en
appliquant la formule d'Euler-Lagrange :
- a)Pendule pesant simple
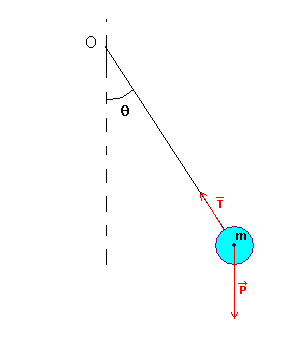
On peut établir l'équation différentielle du mouvement d'oscillation simplement à partir de la conservation de l'énergie mécanique. En négligeant les frottements, l'énergie mécanique du pendule est constante: elle est la somme de l'énergie cinétique et de l'énergie potentielle.
Dans le cas du modèle du pendule pesant simple, on considère que l'objet se ramène à une masse ponctuelle m, qui se déplace à la distance l de l'axe (longueur du fil ou de la tige, considérée inextensible et sans masse). On en déduit:
 avec
avec 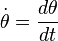
- g est l'accélération de la pesanteur.
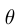 est l'angle que fait le pendule, avec la verticale, à un temps t
est l'angle que fait le pendule, avec la verticale, à un temps t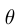 (0) est l'angle maximal.
(0) est l'angle maximal.
L'énergie mécanique étant constante dans le temps, sa dérivée est nulle. En dérivant la relation ci-dessus par rapport au temps on obtient après simplification:
-

Cette équation est celle d'un oscillateur non harmonique, c’est-à-dire non sinusoïdal.
La période T des oscillations dépend de l'amplitude du mouvement.
Par contre, la période ne dépend pas de la masse.
Pour de faibles oscillations, l'équation différentielle peut approximativement s'écrire:
-

On voit donc que, pour de faibles amplitudes permettant d'approcher le sinus à son angle, le pendule se comporte comme un oscillateur harmonique. La période est alors indépendante de l'amplitude. On appelle ceci l'isochronisme des petites oscillations. Cette période s'exprime alors simplement par:

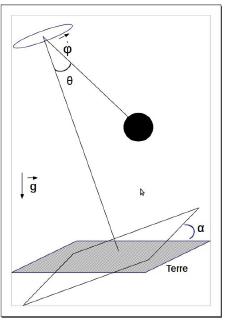
- b)Cas d'un pendule tournant
Nous prendrons pour notre pendule les paramètres suivants longueur
L=1m,la force g=9.8 S.I, 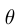 angle de
rotation du pendule autour de son axe ,
angle de
rotation du pendule autour de son axe , 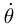 vitesse de rotation du
pendule par rapport a l'axe z, et
vitesse de rotation du
pendule par rapport a l'axe z, et 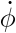 vitesse de
vitesse de
rotation du système autour de l'axe z.
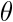 :
:
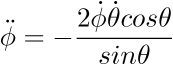
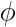 :
:
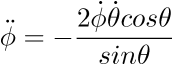
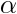 inclinaison du pendule par rapport à la gravité.
inclinaison du pendule par rapport à la gravité.

 avec
avec 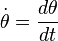



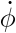 vitesse de
vitesse de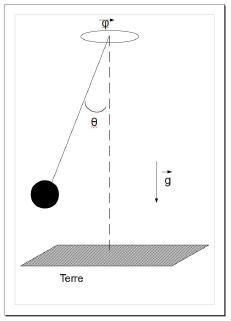
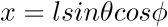
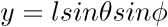
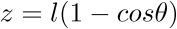
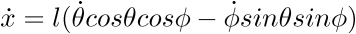
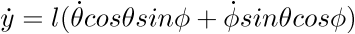
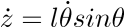
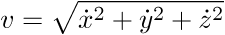 ----->
----->
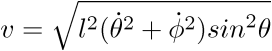
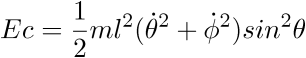
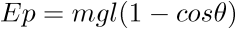
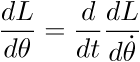
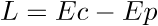
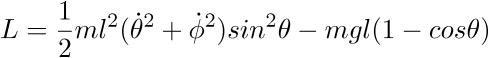
 et
et